Trigonometría
¿Para qué sirve?
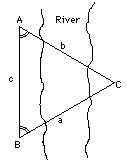 Está cerca de un ancho río y necesita conocer la distancia hasta la otra orilla, digamos hasta el árbol marcado en el dibujo por la letra C (para simplificar, ignoremos la 3ª dimensión). ¿Cómo hacerlo sin cruzar el río? La forma habitual es como sigue. Clave dos postes en el suelo en los puntos A y B y mida con una cinta la distancia c entre ellos (la "base"). |
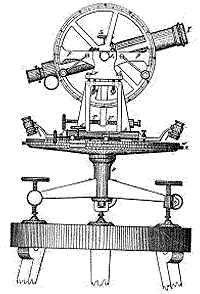 | Un antiguo telescopio
de topógrafo (teodolito). |
| Luego extraiga el poste del punto A y sustitúyalo por un telescopio de topógrafo como el que se muestra aquí ("teodolito"), contando con una placa dividida en 360 grados, marque la dirección ("azimut") a la que apunta el telescopio. Dirigiendo el telescopio primero hacia el árbol y luego hacia el poste B, mide el ángulo A del triángulo ABC, igual a la diferencia entre los números que ha leído de la placa de azimut. Sustituya el poste, lleve el teodolito al punto B y mida de la misma forma el ángulo B . La longitud c de la base y los dos ángulos A y B son todo lo que necesita para conocer el triángulo ABC, suficiente, por ejemplo, para construir un triángulo de la misma forma y mismo tamaño, en un sitio más conveniente. La trigonometría (de trigon = triángulo) en un principio fue el arte de calcular la información perdida mediante simple cálculo. Dada la suficiente información para definir un triángulo, la trigonometría le permite calcular el resto de las dimensiones y de ángulos. |
¿Por qué triángulos? Porque son los bloques básicos de construcción para cualquier figura rectilínea que se pueda construir. El cuadrado, el pentágono u otro polígono puede dividirse en triángulos por medio de líneas rectas radiando desde un ángulo hacia los otros.
Para topografiar una tierra los topógrafos la dividen en triángulos y marcan cada ángulo con un "punto de referencia", que hoy en día es, a menudo, una placa de latón redonda fijada en el suelo con un agujero en el centro, sobre el que ponen sus varillas y teodolitos (George Washington hizo este trabajo cuando era un adolescente). Después de medir la base, como la AB en el ejemplo del río, el topógrafo medirá (de la forma descrita aquí) los ángulos que se forman con el punto C y usar la trigonometría para calcular las distancias AC y BC. Estas pueden servir como base de 2 nuevos triángulos, que a su vez suministrarán bases para dos más..., y de esta forma construirá más y más triángulos hasta que se cubra la tierra al completo con una red que tiene distancias conocidas. Posteriormente se puede añadir una red secundaria, subdividiendo los triángulos grandes y marcando sus puntos con estacas de hierro, que proporcionarán distancias conocidas adicionales en las que se pueden basar los mapas o los planos. Un gran proyecto de reconocimiento de los 1800s fue la "Gran Planimetría Trigonométrica" de la India británica. Se construyeron para el proyecto los mayores teodolitos, monstruos con escalas circulares de 36" de ancho, cuyas lecturas se hacían con extraordinaria precisión con 5 microscopios. Cada uno con su caja pesaba media tonelada y se necesitaban 12 hombres para trasladarlo. Usándolos el proyecto cubrió el país con múltiples cadenas de triángulos en las direcciones norte-sur y este-oeste (las áreas entre las cadenas de dejaron para más tarde) y se necesitaron décadas para completarla. En 1843 Andrew Scott Waugh se encargó del proyecto como Inspector General y puso especial atención a las montañas del Himalaya del norte de la India. Debido a las nubes y a la niebla, esas montañas se ven raramente desde las tierras bajas, y hasta 1847 no se consiguieron varias mediciones. Después de haberse hecho, los resultados necesitaron ser analizados laboriosamente por "computadores" en las oficinas de inspección; no eran máquinas sino personas que efectuaban los cálculos trigonométricos. La historia dice que en 1852 el jefe de los "computadores" fue hacia el director y le dijo: "Señor, hemos descubierto la mayor montaña del mundo". Desde una distancia de más de 100 millas (160 km), se observó la montaña desde seis estaciones diferentes, y "no dio lugar a que el observador sospechara que estaba viendo a través de su telescopio el punto más alto de la Tierra". Al principio se la designó como "Pico XV" por la inspección, pero en 1856 Waugh la denominó en memoria de Sir George Everest, su predecesor en la oficina de jefe de inspectores. El Everest fue el primero en registrarse y en usar los teodolitos gigantes; ahora están expuestos en el "Museum of the Survey of India" en Dehra Dum. Hoy en día la posición sobre la Tierra se puede localizar de forma muy precisa usando el sistema de posicionamiento global (GPS) de 24 satélites en órbita exacta, que están difundiendo constantemente su posición. Un pequeño instrumento electrónico de mano recibe sus señales y nos devuelve nuestra posición con un error de 10-20 metros ( aún es más preciso para usos militares, los patrocinadores del sistema). Se usa una gran cantidad de trigonometría, pero lo hace todo la computadora que está dentro de su aparato, lo único que usted necesita es pulsar los botones apropiados. |
Trigonometría, rama de las matemáticas que estudia las relaciones entre los lados y los ángulos de los triángulos. Etimológicamente significa `medida de triángulos'.
Las primeras aplicaciones de la trigonometría se hicieron en los campos de la navegación, la geodesia y la astronomía, en los que el principal problema era determinar una distancia inaccesible, es decir, una distancia que no podía ser medida de forma directa, como la distancia entre la Tierra y la Luna. Se encuentran notables aplicaciones de las funciones trigonométricas en la física y en casi todas las ramas de la ingeniería, sobre todo en el estudio de fenómenos periódicos, como el flujo de corriente alterna.
Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias aestrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites.
Razones trigonométricas
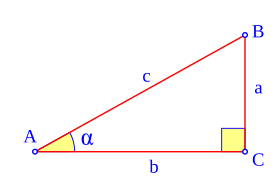
El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo  , correspondiente al vértice A, situado en el centro de la circunferencia.
, correspondiente al vértice A, situado en el centro de la circunferencia.
- El seno (abreviado como sen, o sin por llamarse "sinus" en latín) es la razón entre el cateto opuesto y la hipotenusa,
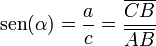
- El coseno (abreviado como cos) es la razón entre el cateto adyacente y la hipotenusa,

- La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto y el adyacente,
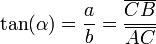
Razones Trigonométricas Recíprocas
Se definen la cosecante, la secante y la cotangente, como las razones recíprocas al seno, coseno y tangente, del siguiente modo:
- cosecante: (abreviado como csc o cosec) es la razón recíproca de seno, o también su inverso multiplicativo:

- secante: (abreviado como sec) es la razón recíproca de coseno, o también su inverso multiplicativo:

- cotangente: (abreviado como cot o cta) es la razón recíproca de la tangente, o también su inverso multiplicativo:

Normalmente se emplean las relaciones trigonométricas seno, coseno y tangente, y salvo que haya un interés especifico en hablar de ellos o las expresiones matemáticas se simplifiquen muchísimo, los términos cosecante, secante y cotangente no suelen utilizarse.
Funciones trigonométricas inversas
En trigonometría, cuando el ángulo se expresa en radianes (dado que un radián es el arco de circunferencia de longitud igual alradio), suele denominarse arco a cualquier cantidad expresada en radianes; por eso las funciones inversas se denominan con el prefijo arco, así si:

y es igual al seno de x, la función inversa:

x es el arco cuyo seno vale y, o también x es el arcoseno de y.
si:

y es igual al coseno de x, la función inversa:

x es el arco cuyo coseno vale y, que se dice: x es el arcocoseno de y.
si:

y es igual al tangente de x, la función inversa:
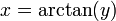
x es el arco cuya tangente vale y, ó x es igual al arcotangente de y.
Valor de las funciones trigonométricas
A continuación algunos valores de las funciones que es conveniente recordar:
Para el calculo del valor de las funciones trigonométricas se confeccionaron tablas trigonométricas. La primera de estas tablas fue desarrollada por Johann Müller Regiomontanoen 1467, que nos permiten, conocido un ángulo, calcular los valores de sus funciones trigonométricas. En la actualidad dado el desarrollo de la informática, en prácticamente todos los lenguajes de programación existen librerías de funciones que realizan estos cálculos, incorporadas incluso en calculadoras electrónicas de bolsillo, por lo que el empleo actual de las tablas resulta obsoleto.
Sentido de las funciones trigonométricas
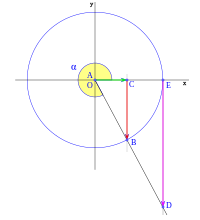
Dados los ejes de coordenadas cartesianas xy, de centro O, y una circunferencia goniométrica (circuferencia de radio la unidad) con centro en O; el punto de corte de la circunferencia con el lado positivo de las x, lo señalamos como punto E.
Notese que el punto A es el vertice del triangulo, y O es el centro de coordenada del sistema de referencia:
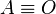
a todos los efectos.
La recta r, que pasa por O y forma un ángulo  sobre el eje de las x, corta a la circunferencia en el punto B, la vertical que pasa por B, corta al eje x en C, la vertical que pasa por E corta a la recta r en el punto D.
sobre el eje de las x, corta a la circunferencia en el punto B, la vertical que pasa por B, corta al eje x en C, la vertical que pasa por E corta a la recta r en el punto D.
Por semejanza de triángulos:
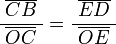
Los puntos E y B estan en la circunferencia de centro O, por eso la distancia  y
y  son el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas:
son el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas:

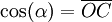

tenemos:

La tangente es la relación del seno entre el coseno, según la definición ya expuesta.
Primer cuadrante
Partiendo de esta representación geométrica de las funciones trigonométricas, podemos ver las variaciones de las funciones a medida que aumenta el ángulo a.
Para 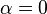 , tenemos que A, C, y D coinciden en B, por tanto:
, tenemos que A, C, y D coinciden en B, por tanto:



Si aumentamos progresivamente el valor de  , las distancias
, las distancias  y
y 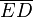 aumentaran progresivamente, mientras que
aumentaran progresivamente, mientras que  disminuirá.
disminuirá.
Percatarse que  y
y  están limitados por la circunferencia y por tanto su máximo valor absoluto será 1, pero
están limitados por la circunferencia y por tanto su máximo valor absoluto será 1, pero 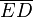 no está limitado, dado que D es el punto de corte de la recta r que pasa por O, y la vertical que pasa por E, en el momento en el que el ángulo
no está limitado, dado que D es el punto de corte de la recta r que pasa por O, y la vertical que pasa por E, en el momento en el que el ángulo  rad, la recta r será la vertical que pasa por O. Dos rectas verticales no se cortan, o lo que es lo mismo la distancia
rad, la recta r será la vertical que pasa por O. Dos rectas verticales no se cortan, o lo que es lo mismo la distancia 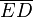 será infinita.
será infinita.
La tangente toma valor infinito cuando  rad, el seno vale 1 y el coseno 0.
rad, el seno vale 1 y el coseno 0.
Segundo cuadrante
Cuando el ángulo  supera el ángulo recto, el valor del seno empieza a disminuir según el segmento
supera el ángulo recto, el valor del seno empieza a disminuir según el segmento  , el coseno aumenta según el segmento
, el coseno aumenta según el segmento  , pero en el sentido negativo de las x, el valor del coseno toma sentido negativo, si bien su valor absoluto aumenta cuando el ángulo sigue creciendo.
, pero en el sentido negativo de las x, el valor del coseno toma sentido negativo, si bien su valor absoluto aumenta cuando el ángulo sigue creciendo.
La tangente para un ángulo  inferior a
inferior a  rad se hace infinita en el sentido positivo de las y, para el ángulo recto la recta vertical r que pasa por O y la vertical que pasa por E no se cortan, por lo tanto la tangente no toma ningún valor real, cuando el ángulo supera los
rad se hace infinita en el sentido positivo de las y, para el ángulo recto la recta vertical r que pasa por O y la vertical que pasa por E no se cortan, por lo tanto la tangente no toma ningún valor real, cuando el ángulo supera los  rad y pasa al segundo cuadrante la prolongación de r corta a la vertical que pasa porE en el punto D real, en el lado negativo de las y, la tangente
rad y pasa al segundo cuadrante la prolongación de r corta a la vertical que pasa porE en el punto D real, en el lado negativo de las y, la tangente 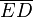 por tanto toma valor negativo en el sentido de las y, y su valor absoluto disminuye a medida que el ángulo
por tanto toma valor negativo en el sentido de las y, y su valor absoluto disminuye a medida que el ángulo  aumenta progresivamente hasta los
aumenta progresivamente hasta los  rad.
rad.
Resumiendo: en el segundo cuadrante el seno de  ,
,  , disminuye progresivamente su valor desde 1, que toma para
, disminuye progresivamente su valor desde 1, que toma para  rad, hasta que valga 0, para
rad, hasta que valga 0, para  rad, el coseno,
rad, el coseno, , toma valor negativo y su valor varia desde 0 para
, toma valor negativo y su valor varia desde 0 para  rad, hasta –1, para
rad, hasta –1, para  rad.
rad.
La tangente conserva la relación:

incluyendo el signo de estos valores.
Tercer cuadrante
En el tercer cuadrante, comprendido entre los valores del ángulo  rad a
rad a  rad, se produce un cambio de los valores del seno el coseno y la tangente, desde los que toman para
rad, se produce un cambio de los valores del seno el coseno y la tangente, desde los que toman para  rad:
rad:



Cuando el ángulo  aumenta progresivamente, el seno aumenta en valor absoluto en el sentido negativo de las y, el coseno disminuye en valor absoluto en el lado negativo de las x, y la tangente aumenta del mismo modo que lo hacia en el primer cuadrante.
aumenta progresivamente, el seno aumenta en valor absoluto en el sentido negativo de las y, el coseno disminuye en valor absoluto en el lado negativo de las x, y la tangente aumenta del mismo modo que lo hacia en el primer cuadrante.
A medida que el ángulo crece el punto C se acerca a O, y el segmento  , el coseno, se hace más pequeño en el lado negativo de las x.
, el coseno, se hace más pequeño en el lado negativo de las x.
El punto B, intersección de la circunferencia y la vertical que pasa por C, se aleja del eje de las x, en el sentido negativo de las y, el seno,  .
.
Y el punto D, intersección de la prolongación de la recta r y la vertical que pasa por E, se aleja del eje las x en el sentido positivo de las y, con lo que la tangente,  , aumenta igual que en el primer cuadrante
, aumenta igual que en el primer cuadrante
Cuando el ángulo  alcance
alcance  rad, el punto C coincide con O y el coseno valdrá cero, el segmento
rad, el punto C coincide con O y el coseno valdrá cero, el segmento  será igual al radio de la circunferencia, en el lado negativo de las y, y el seno valdrá –1, la recta r del ángulo y la vertical que pasa por E serán paralelas y la tangente tomara valor infinito por el lado positivo de las y.
será igual al radio de la circunferencia, en el lado negativo de las y, y el seno valdrá –1, la recta r del ángulo y la vertical que pasa por E serán paralelas y la tangente tomara valor infinito por el lado positivo de las y.
El seno el coseno y la tangente siguen conservando la misma relación, tanto en valores como en signo, nótese que cuando el coseno vale cero, la tangente se hace infinito.
Cuarto cuadrante
En el cuarto cuadrante, que comprende los valores del ángulo  entre
entre  rad y
rad y  rad, las variables trigonométricas varían desde los valores que toman para
rad, las variables trigonométricas varían desde los valores que toman para  rad:
rad:



hasta los que toman para  rad pasando al primer cuadrante, completando una rotación:
rad pasando al primer cuadrante, completando una rotación:



como puede verse a medida que el ángulo  aumenta, aumenta el coseno
aumenta, aumenta el coseno  en el lado positivo de las x, el seno
en el lado positivo de las x, el seno  disminuye en el lado negativo de las y, y la tangente
disminuye en el lado negativo de las y, y la tangente 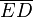 también disminuye en el lado negativo de las y.
también disminuye en el lado negativo de las y.
Cuando  , vale
, vale  ó
ó  al completar una rotación completa los puntos B, C y D, coinciden en E, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante.
al completar una rotación completa los puntos B, C y D, coinciden en E, haciendo que el seno y la tangente valga cero, y el coseno uno, del mismo modo que al comenzarse el primer cuadrante.
Representación gráfica

Representación de las funciones trigonométricas en el plano xy, los valores en el eje x multiplicados por πRadián.
Identidades trigonométricas
Una identidad es una igualdad en que se cumple para todos los valores permisibles de la variable. En trigonometría existen cinco identidades fundamentales:
Recíprocas



De división

Por el teorema de Pitágoras
Como en el triángulo rectángulo se cumple que:

de la figura anterior se tiene que:
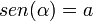
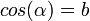

entonces para todo ángulo α, se cumple la identidad Pitagórica :

que tambien puede expresarse:


Suma y diferencia de dos ángulos
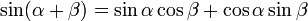





Suma y diferencia del seno y coseno de dos ángulos




Producto del seno y coseno de dos ángulos
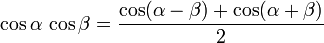

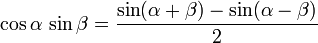

Ángulo doble
- sen(2α) = 2 sen α cos α
- cos(2α) = cos2α - sen2α
- cos(2α) = 1 – 2 sen2(α)
- cos(2α) = 1 + 2 cos2(α)
Otras identidades trigonométricas
- sen (90 – α) = cos α
- cos (90 – α) = sen α
- sen (180 – α) = sen α
- cos (180 – α) = –cos α
- sen α cosα + sen β cos β = sen(α + β)Cos(α - β)
Función tangente
En un triángulo rectángulo, la tangente (abreviada como tan o tg) es la razón entre el cateto opuesto y el cateto adyacente.

El valor de la tangente para algunos ángulos importantes es:
- tan = AC / OA = BD / OB = sen / cos
- tan (π/2) = tan (90°) = +∞
- tan (-π/2) = tan (-90°) = -∞
- tan (0) = 0
- tan (π/4) = tan (45°) = 1
- tan (π/3) = tan (60°)=
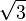
- tan (π/6) = tan (30°) =
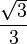
Una identidad de importancia con la tangente es:

Seno y Coseno, funciones complejas
El seno y coseno se define en matemática compleja , gracias a la fórmula de Euler como:
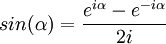

Por lo tanto, la tangente quedará definida como:
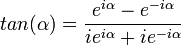
Siendo 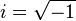 (también puede representarse como j)
(también puede representarse como j)
TRIGONOMETRÍA PLANA
Se ocupa fundamentalmente de la resolución de triángulos planos. Para ello, se definen las razones trigonométricas de los ángulos y se estudian las relaciones entre ellas.
|
| Razones trigonométricas de ángulos agudos |
La base de la trigonometría está en las razones trigonométricas, valores numéricos asociados a cada ángulo, que permiten relacionar operativamente los ángulos y lados de los triángulos. Las más importantes son seno, coseno y tangente, que se definen a continuación.
En un ángulo a de un triángulo rectángulo, ABC, se llama seno de a, y se escribe sen a, al cociente entre el cateto opuesto y la hipotenusa:
Análogamente se definen el coseno (cos) como cociente entre el cateto adyacente y la hipotenusa, y la tangente (tg) como el cociente entre el cateto opuesto y el cateto adyacente:
Hace no muchos años existían tablas numéricas en las que se daban los valores de las razones trigonométricas de una gran cantidad de ángulos. En la actualidad, con una calculadora científica se obtienen con toda precisión los valores de las razones trigonométricas de cualquier ángulo.
Las razones trigonométricas de un ángulo cumplen las siguientes propiedades:Aunque el ángulo a pertenezca a otro triángulo rectángulo de lados distintos al anterior, los valores obtenidos para sen a, cos ay tg a son los mismos. Es decir, las razones trigonométricas de un ángulo no dependen del triángulo sobre el que se midan. Esto es debido a que dos triángulos rectángulos con un mismo ángulo agudo son semejantes y, por tanto, los cocientes, a/c, b/c, a/bcoinciden en ambos.
Las razones trigonométricas sen y cos de un mismo ángulo guardan la siguiente relación fundamental:
En vez de (sen a)2 se acostumbra a escribir sen2 a, y lo mismo con las demás razones trigonométricas. Por eso, la igualdad anterior se suele expresar así:
Las razones sen a, cos a y tg a se relacionan entre sí del siguiente modo:
|
| Razones trigonométricas de ángulos cualesquiera |
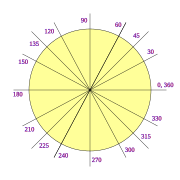
Para definir las razones trigonométricas de ángulos cualesquiera (de 0º a 360º) se empieza situando el ángulo en la llamada circunferencia goniométrica, una circunferencia de radio 1 con su centro, O, situado sobre unos ejes coordenados:
El vértice del ángulo se sitúa en O y el primero de sus lados, a, sobre la parte positiva del eje de las X. El segundo lado, b, se abre girando en sentido contrario a las agujas del reloj. Este segundo lado corta a la circunferencia goniométrica en un punto, P, cuyas coordenadas son c = cos a y s = sen a. Es decir, P(cos a, sen a). La tg a= t se sitúa sobre la recta r, tangente a la circunferencia en U, y queda determinada por el punto T en que el lado b, o su prolongación, corta a r.
Según esta definición, las razones trigonométricas sen, cos y tg toman valores positivos o negativos según el cuadrante en el que se encuentre el ángulo a. En la figura siguiente se resumen los signos de las tres razones:
Los ángulos 90º y 270º no tienen tangente, pues para ellos el segundo lado no corta a la recta r.
Las razones trigonométricas de ángulos no agudos cumplen las mismas relaciones que las de los ángulos agudos:
|
| Otras razones trigonométricas |
A partir de las razones trigonométricas sen, cos y tg se definen la cosecante (cosec), la secante (sec) y la cotangente (cot) del siguiente modo:
Estas razones trigonométricas no están definidas cuando el denominador es cero. Por ejemplo, sec a no está definida para a = 90º ni para a = 270º, pues cos 90º = 0 y cos 270º = 0.
La cotangente es cero donde la tangente no está definida, es decir, cot 90º = 0 y cot 270º = 0.
Fuentes:
http://html.rincondelvago.com/trigonometria_9.html
http://www.phy6.org/stargaze/Mtrig1.htm
1. ↑ Etimología de la palabra "trigonometría". Diccionario web de etimología (inglés).
http://es.wikipedia.org/wiki/Cosecante#F.C3.B3rmulas_trigonom.C3.A9tricas_elementales
http://es.encarta.msn.com/encnet/refpages/RefArtTextonly.aspx?refid=761572350&print=7




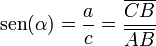

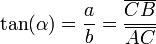








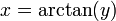









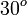


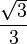
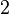
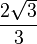





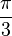
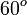



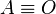
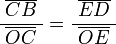
 y
y  son el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas:
son el radio de la circunferencia, en este caso al ser una circunferencia de radio = 1, y dadas las definiciones de las funciones trigonométricas:
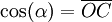




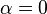 , tenemos que
, tenemos que 


 y
y 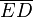 aumentaran progresivamente, mientras que
aumentaran progresivamente, mientras que  disminuirá.
disminuirá.
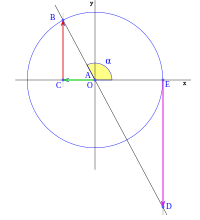




















 al completar una rotación completa los puntos
al completar una rotación completa los puntos 





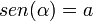
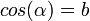




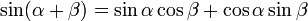









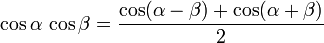

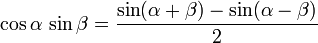


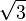

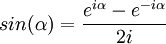

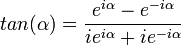
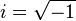 (también puede representarse como
(también puede representarse como 






